T检验
T检验（TTest）
什么是T检验
T检验，亦称studentt检验（Student"sttest），主要用于样品含量低(例如)n<30)总体标准差σ未知的正态分布数据。
T检验这是一种检验小样本(样本容量小于30)两个平均量小于30）。它是用来检验的T分布理论推断差异的概率，从而判断两个平均值的差异是否明显。
T检验是戈斯特为观察酿酒质量而发明的。戈斯特是都柏林健力士酿酒厂的统计学家。戈斯特于1908年在Biometrika上公布T但由于老板认为是商业秘密，被迫使用笔名(学生)。
T检验的适用条件：正态分布数据
单个样本的t检验
目的：比较样本均数所代表的未知总体均数μ和已知的总体平均值μ0。
计算公式：
t统计量：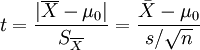
自由度：v=n-1
适用条件：
(1)已知总体均数；
(2)样本得到样本平均值和样本标准误差；
(3)样本来自正态或近似正态。
单个样本的t检验实例分析
例1难产儿出生体重
婴儿出生出生体重μ0=3.30(获得大规模调查)，问是否相同？
解：1.建立假设，确定检验水平α
H0:μ=μ0(难产儿等于一般婴儿出生体重总数；H0无效假设，nullhypothesis）
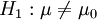(难产儿与一般婴儿出生体重总数不同；H1备择假设，alternativehypothesis，）
双侧检验，检验水平：α=0.05
2.计算检验统计
3.确定相应的界值表P值，下结论
查附表1:t0.05/2.34=2.032,t=1.77,t<t0.05/2.34,P>0.05,按α=0.05水平，不拒绝H0，两者之间的差异没有统计意义，难产儿的平均出生体重与普通婴儿不同
配对样本t检验
配对设计：根据类似的原则，将受试者的一些重要特征配对，以消除混合因素的影响。除处理因素/研究因素外，一对观察对象之间的其他因素基本相同，每对两个人随机处理两种。
- 两种同质对象分别接受性别、年龄、体重、病情程度等两种不同的治疗。
- 同一受试者或同一样本的两部分分别接受两种不同的处理
- 自我比较。即比较同一受试者处理前后的结果。
目的：判断不同的处理是否有差异
计算公式及意义：
t统计量：
自由度：v=对子数-1
适用条件：配对数据
T检验的步骤
建立虚无假设H0:μ1=μ2，即先假定两个总体平均数之间没有显着差异；
2.计算统计量t对于不同类型的问题，选择不同的统计计算方法；
1)如果要评估小样本平均值与整体平均值的差异，则其统计量t值的计算公式为：
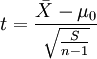
2)如果要评估两组样本平均值之间的差异，则其统计量t值的计算公式为：
3.根据自由度df=n-1，查t值表，找出规定的t理论值并进行比较。理论值差异的显著水平为0.01级或0.05级。不同自由度的显著水平理论值被记录为t(df)0.01和t(df)0.05
4.比较计算得到的t值和理论t根据下表给出的值，推断发生的概率t判断值与差异显著关系表。
5.根据以上分析，结合具体情况得出结论。
T说明检验例子
例如，T检查可用于比较药物治疗组和安慰剂治疗组患者的测量差异。理论上，即使样本量很小，也可以进行T测试。（如果样本量为10，一些学者声称甚至更小的样本也可以），只要每组中的变量呈正态分布，两组之间的方差就不会明显不同。如上所述，可以通过观察数据的分布或正态测试来估计数据的正态假设。可以进行方差齐的假设F检查或更有效Levene"s检查。如果不符合这些条件，必须用非参数检查代替T检查比较两组间均值。
T检验中的P值是接受两个平均值之间的差异的概率。在统计学中，当两组观察对象之间没有差异时，这个概率与我们拒绝假设有关。一些学者认为，如果差异有特定的方向，我们只需要考虑单边概率分布t-检验的P值分为两半。另一些学者认为，在任何情况下都应该报告标准的双侧T检验概率。
1.数据排列
独立样本T测试需要一个自(分组)变量(如性别:男女)和一个因变量(如测量值)。根据自变量的特定值，比较每组因变量的平均值。T比较以下男女身高平均值。
2、T检验图
在T在检验过程中，可以直观地看到平均值和方差的比较，见下图：
这些图表可以快速估计并直观地显示分组变量与变量相关的强度。
三、多组间比较
科研实践中，经常需要进行两组以上比较，或含有多个自变量并控制各个自变量单独效应后的各组间的比较，（如性别、药物类型与剂量），此时，需要用方差分析进行数据分析，方差分析被认为是T推广检验。在复杂的设计中，方差分析有很多t-检验所没有的优点。T比较设计中不同格子平均值的检验)。
T检查注意事项
- 随机、均衡、可比的严格抽样设计
- 所选检验方法必须符合适用条件(注:t检验的前提是数据服从正常分布)
- 单侧检查和双侧检查
单侧检查的边界值小于双侧检查的边界值，因此更容易拒绝和犯第Ⅰ错误的可能性很大。
- 假设检验结论不能绝对化
- 不能拒绝H0，样本数量可能不够拒绝H0，有可能犯第Ⅰ类错误
- 正确理解P统计学是否有意义？
P越小并不意味着实际差异越大，而是越有理由拒绝H0.越有理由表明两者之间存在差异，统计学和专业的实际意义是否不完全相同
- 假设检验与可信区间的关系
- 结论是一致的
- 差异：提供不同的信息
区间估计给出整体平均值的可能值范围，但不给出确切的概率值，假设可以给出检查H是否成立的概率
参考文献
- ↑宇传华.医学等本科班《医学统计》第三章两组资料平均比较22010.12.1
- ↑李克东编着.第十三章SPSS教材教育技术研究方法应用教育技术学主要课程系列.2003年4月，北京师范大学出版社第一版.
T检验
T检验发表于2022-06-15，由周林编辑，文章《T检验》由admin于2022年06月15日发布于本网，共2201个字，共5160人围观，目录为外贸知识，如果您还要了解相关内容敬请点击下方标签，便可快捷查找与文章《T检验》相关的内容。
版权声明：
文章:(T检验)，来源：，阅读原文。
T检验若有[原创]标注，均为本站原创文章，任何内容仅供学习参考，未经允许不得转载，任何内容不得引用，文章若为转载文章，请注明作者来源，本站仅为分享知识，不参与商业活动，若有侵权请联系管理删除
微信扫一扫打赏
支付宝扫一扫打赏
